Prop Efficiency

This section will have a couple of places where the definitions and conclusions are different from those in most model airplane literature -- and web sites. They are not different from those used in aircraft engineering practice and the standard concepts of mechanics. The first of these is the definition of efficiency.

The efficiency of a propeller in any flight condition is the ratio of the thrust power delivered to the shaft power required to turn it. It is not the "slip" which is often described as the difference between some measured blade element pitch and the pitch of the flight helix. The thrust power is just the product of the part of propeller thrust applied in the direction of flight and the aircraft speed. For US readers the "English" units of power are    foot-pounds/second  for most of the rest of the world the unit is   watts .

For example 10  pounds of thrust at 55   feet/second  produces
10*55 = 550    foot-pounds/second  , i.e. one horsepower.

There is a lot more said about model airplane propeller efficiency than is known. Aside from what is known from full scale engineering practice and the anecdotal evidence from flying as a community we have little else. There is, however, at least one real wind tunnel test of a model airplane propeller. If anyone else has other examples I'd be very glad to see them. The test of reference was made in association with RPV/UAV studies done for the Army. The results were appalling. Though admittedly the propellers today certainly are better in every way when compared to those of the 1980's and previously, the results were still a shocker. A Top Flite 10-6 for example approached 60% efficiency in only one flight condition and more usually efficiency was in the region of 50%. Large aircraft propellers in cruise are typically near 90% efficient.

Clearly, the drag of the propeller blade reduces propeller efficiency, however as discussed in the previous section, the inflow also reduces the efficiency. One way or seeing that this is true is to notice that inflow makes the flow come in to the propeller at a steeper angle. This tilts the lift of the blade back in the drag direction.

As typically derived in textbooks, however, the propeller thrust is shown to be the rate at which momentum is imparted to the slipstream, that is, the mass flow rate times the increase in slip stream velocity. The thrust power is the aircraft velocity times this thrust.

The energy required to accelerate the slipstream is the mass flow rate times the increase in the square of the velocity in the slipstream, that is, the rate of kinetic energy increase. It is always larger than the thrust power and the difference increases with increasing inflow velocity.

Because of this, it is always better to accelerate a large mass a small amount than a small mass a great deal. This explains the large diameter rotors on helicopters and the large reduction gearing used on large aircraft propellers.

An example will help. No propeller blade drag effects, just the induced efficiency.

• Airplane flies at V = 100 ft/sec
• Slipstream increase in velocity (2 cases)
  1. v = 10 ft/sec
  2. v = 20 ft/sec
• Increase in momentum
  1. Vv = 100 * 10 = 1000
  2. Vv = 100 * 20 = 2000
• Increase in kinetic energy
  1. 0.5*[(V+v)²-V²] = 0.5*[110²-100²] = 1050
  2. 0.5*[(V+v)²-V²] = 0.5*[120²-100²] = 2200
• Induced efficiency
  1. 1000/1050 = 0.952
  2. 2000/2200 = 0.909

The induced efficiency computed above is an upper bound and real induced efficiency will surely be less. More blades improves the induced efficiency on large aircraft where blade drag is small. On model aircraft the improvement in airfoil performance with the wider chord of a 1-blade propeller usually more than pays for any efficiency loss. Typical results for model airplanes with high quality, properly matched propellers may have the induced efficiency (loss due to inflow) of 96% to 90% and due to propeller drag alone of 70% to 80% for a net efficiency somewhere between 80% and 60%.

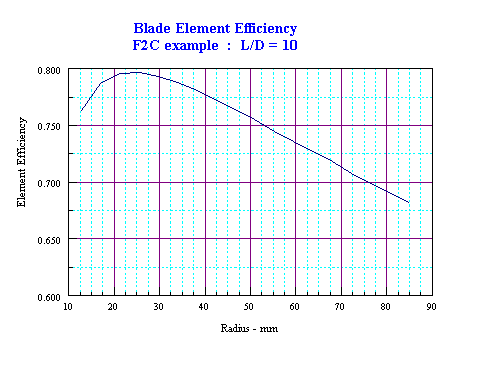
As an example, the efficiency of each blade element assuming a lift-to-drag ration of 10 and a constant inflow distribution for an example F2C prop is shown below. Note that the best efficiency is near the root so that smaller diameters may bring a minor performance increase.>

There is one aspect of propeller efficiency that has not received much attention. If the propeller is at the rear of the vehicle then the efficiency can be higher. The only common flying example of this is the Cessna 337 "push-pull" twin engine Super Skymaster. The engines are identical and the aircraft engine-out performance is distinctly better with the pusher engine than the tractor. The most successful example was the experimental Douglas XB-42 "Mixmaster". this aircraft had two Allison V1710 engines in the fuselage driving a contrarotating propeller behind the horizontal tail. The performance was very good and, although the jet age arrived and the bomber was not procured.

Douglas designed a private aircraft at the end of the war using the same configuration. This aircraft, the Douglas "Cloudster", was a failure. As I understand it there were problems in both the drive train and aerodynamics. The aerodynamicist who was assigned to work on it after it was in flight test told me of the many fixes they tried, however the judgment was that the flow approaching the propeller was not sufficiently uniform.

In the right configuration a pusher has been estimated to be 5% to 10% better. This is because: (1) The accelerated airflow behind the propeller does not wash over the fuselage (the inflow still does, however). (2) The inflow and reduced pressure in front of the prop can help keep the boundary layer attached. (3) The propeller accelerates some of the flow that was retarded by drag. This is inherently more efficient.